Le versioni classiche della fisica e della geometria, che vengono insegnate a chi non intraprende studi universitari in quell’ambito (cioè la quasi totalità delle persone comuni), descrivono leggi che non si applicano all’infinitamente grande e l’infinitamente piccolo, cioè a tutto ciò che esiste al di là del sistema di riferimento-uomo.
Ad esempio la fisica classica (con Newton e la sua meccanica), non è in grado di spiegare il comportamento della materia a livello atomico/subatomico o il moto dei corpi quando la sua velocità si approssima a quella della luce.
Ma se non siamo così ambiziosi da volerci cimentare con la meccanica quantistica che, invece, quella spiegazione è in grado di darcela, siamo però abbastanza grandi per apprendere che le tre certezze di geometria euclidea che avevamo crollino, quando si passa da un foglio di carta ad una realtà in scala cosmica.
Così apprendiamo che : 1) la somma degli angoli di un triangolo è sempre superiore a 180 gradi; 2) per un punto esterno ad una retta non può passare nessuna retta parallela alla prima; 3) tutte le rette si incontrano in due punti opposti.
La spiegazione di questa contraddizione sta tutta nella curvatura. La realtà è curva. La Terra è una sfera(1). Come possono esistere, quindi, nella realtà due rette parallele che non si incontrano mai se la superficie della Terra è sferica? Tracciare rette parallele su una sfera non è possibile. Anche i Meridiani, che sono linee immaginarie create per convenzione, finiscono inevitabilmente col non essere né rette, né parallele (tanto che si incrociano, eccome, nei due Poli).
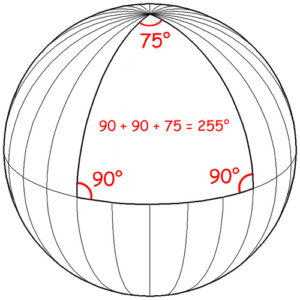
(Proprietà di un triangolo disegnato su una sfera)
Tali geometrie, di cui abbiamo sopra accennato solo alcuni degli elementi fondanti, si definiscono geometrie non Euclidee ed includono la geometria iperbolica e la geometria ellittica.
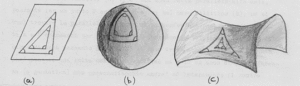
(differenze tra triangoli rispettivamente in geometria Euclidea, ellittica e iperbolica)
La loro definizione, agli inizi dell’Ottocento, è stata fondamentale per l’elaborazione della teoria della relatività generale di Einstein ed in particolare l’introduzione del concetto di curvatura dello spazio-tempo. Secondo Einstein a governare l’interazione tra masse, quali quelle dei pianeti, non è il principio della fisica classica che due corpi siano attratti tra loro da una forza direttamente proporzionale alle masse e inversamente proporzionale al quadrato della distanza, ma proprio la curvatura dello spazio-tempo.
La metafora più efficace per spiegare questo concetto è quella del tappeto elastico, che viene più o meno deformato da sfere di massa differente.
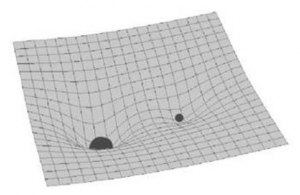
(Curvatura dello spazio-tempo in relazione alle masse dei corpi)
In conclusione, il mondo e l’universo sono governati da leggi diverse da quelle spiegate dalla meccanica classica e dalla geometria euclidea, che funzionano solo su scale né troppo piccole, né troppo grandi (non l’atomo, non i pianeti). Per tutto il resto ci sono la meccanica quantistica (molto piccolo) e le geometrie non euclidee (molto grande).
(1) non una sfera perfetta ma uno sferoide oblato.
*Questo articolo, come tutto ciò che viene pubblicato su amorvacui.it, non ha alcuna pretesa di divulgazione scientifica, ma solo l’obiettivo di fornire, attraverso semplificazioni strumentali, un invito alla riflessione e all’approfondimento presso fonti che abbiano, al contrario, piena dignità scientifica.
